Transformaciones Geométricas Básicas.
En este apartado veremos las operaciones de transformación que se pueden aplicar a objetos para reubicarlos o dar es un tamaño diferente.
Estas operaciones también son usadas en la visualización de rutinas que convierten una descripción de un sistema de coordenadas universales en un despliegue para un dispositivo de salida. Además, son usados en variedad de otras aplicaciones, tales como diseño de ayuda y animación por computador. Las operaciones que se aplican a descripciones geométricas de un objeto para cambiar su posición, orientación o tamaño se llaman transformaciones geométricas entre otras.
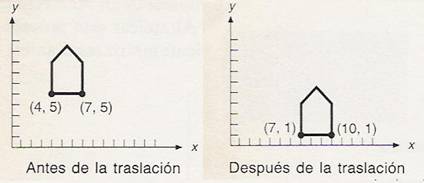
Traslación
Reposiciona un objeto desplazándolo a las nuevas coordenadas, en otras palabras, una traslación se aplica a un objeto para reposicionarlo a lo largo de una línea recta, desde una ubicación de coordenadas a otra.
Representándola en forma cartesiana.
P = (x, y) P'= (x', y')
T = (tx, ty) "El par (t subindice x, t subindice y) se llama vector de traslación"
Representándola en forma matricial.
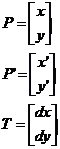
Esto nos permite escribir las ecuaciones de traslación bidimensionales en forma de matriz
para obtener: P'= P +T
Al trasladar cualquier objeto dentro del mundo virtual se debe considerar lo siguientes puntos:
• Es una transformación rígida, el objeto no se deforma
• Para trasladar líneas rectas trasladamos sólo sus extremos
• Para trasladar polígonos, trasladamos sólo sus vértices y redibujamos.
Reflexión
Una transformación que produce la imagen de un objeto en un espejo se llama reflexión. Para una reflexión bidimensional, esta imagen se genera respecto a un eje de reflexión rotando el objeto 180° sobre dicho eje de reflexión.
Esto se puede conseguir con una rotación en 180º, alrededor del eje x ó en el eje y.
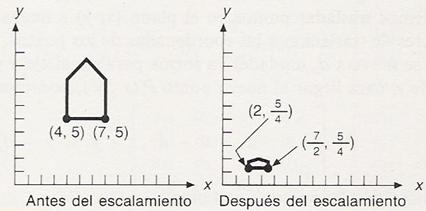
Escalación
La transformación de la escalación altera el tamaño del objeto, esto lo hace escalando
cada uno de sus coordenadas con respecto al origen del eje de coordenadas
Definiendo las coordenadas
x′= x*Sx y′= y*Sy
Sx es la escala en la dirección en x y Sy es la escala en la dirección en y.

donde los parámetros de escalación Sx y Sy se asignan cualesquiera valores positivos.
Los parámetros Sx y Sy escalan un objeto en las direcciones x e y respectivamente.
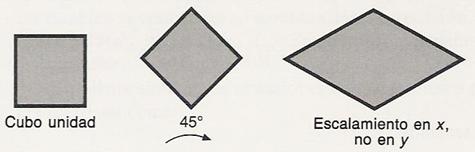
Se puede escalar un objeto en otra dirección, rotando el objeto y alineándolo con el sistema de coordenadas y luego rotándolo en sentido inverso.
Descrito en la siguiente imagen con su respectiva ecuación:
Al escalar cualquier objeto dentro del mundo virtual se debe considerar lo siguientes puntos:
• Si el origen de coordenadas no se encuentra en el interior del objeto, se produce un desplazamiento
Para evitarlo, se usa un punto fijo, y se escala a partir de él. El punto fijo podría ser el centro del objeto, o uno de sus vértices, o también un punto arbitrario.
• Para escalar líneas rectas escalamos sólo sus extremos• Para escalar polígonos, escalamos sólo sus vértices y redibujamos.
Rotación
En rotación, la orientación de ésta puede ser especificada en una variedad de formas, lo que se
explica a continuación es la rotación de un punto con respecto a los ejes fijos. Un eje de
rotación define el polo sobre el cual se va a rotar, como los polos Norte y Sur de la Tierra.
x = r cos teta
y = r sen teta
Rotación alrededor de un punto
Para hacer una rotación general, podemos hacerlo mediante una composición de
transformaciones básicas.
Para generar una rotación se especifica un ángulo de rotación θ y laposición (xr, yr) del punto de rotación (punto pivote) acerca del cual el objeto se rota.
Valores positivos del ángulo de rotación definen una rotación en contra de las agujas del reloj y lo contrario para un ángulo negativo.
En representacion matricial:
P′= R*P
Fuentes
1.-Transformaciones Geometricas
2.-TEMA 3: Transformaciones 2D
3.-CAPÍTULO III: TRANSFORMACIONES GEOMÉTRICAS
4.-CAPITULO 1 Transformaciones Geométricas en dos dimensiones
5.-CAPÍTULO 2 – Modelado y Transformaciones Geométricas


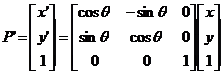

No hay comentarios.:
Publicar un comentario