Aspectos matemáticos de la Graficación
Antes de comenzar, me gustaría citar un fragmento de un libro sobre los fractales.
"le invito a contemplar alguna de las imágenes que más abajo aparecen…
Es fácilmente apreciable, además de su indudable belleza, su semejanza con estructuras naturales con las habitualmente nos tropezamos. Sin embargo, todas ellas son producto de “matemáticas experimentales” (que no aplicadas), o dicho de otro modo, han sido confeccionadas sin salir del laboratorio matemático cuyo material es, esencialmente, un ordenador y algunos conceptos
matemáticos sabiamente utilizados."
Geometría Fractal o el Diseño de la Naturaleza
por: Aniceto Murillo
XXIX Universidad de Otoño
Madrid: España
La geometría fractal ocupa en cierta medida este vacío y puede usarse para diseñar fielmente
desde la intrincada silueta de una simple hoja hasta la evolución del árbol.
Primero para introducirnos al el mundo de los Fractales, lo primero que hay que contar son las palabras que dan inicio al libro "Fractals Everywhere" ("Fractales en todos Lados") de Michael F. Barnsley, uno de los pioneros y más importantes divulgadores e investigadores del tema:
"La geometría Fractal cambiará a fondo su visión de las cosas. Seguir leyendo es peligroso. Se arriesga a perder definitivamente la imagen inofensiva que tiene de nubes, bosques, galaxias, hojas, plumas, flores, rocas, montañas, tapices, y de muchas otras cosas. Jamás volverá a recuperar las interpretaciones de todos estos objetos que hasta ahora le eran familiares."
Ésta geometria tiene su origen en el concepto de proceso iterativo introducido hace ya 300 años por Isaac Newton y Gottfried Leibniz. De forma esquemática, un proceso iterativo consta de: una unidad de entrada compuesta por un dato inicial. Esta unidad de entrada alimenta la unidad de proceso, cerebro pensante del proceso iterativo, que manipula la información recibida y produce un nuevo dato que constituye la unidad de salida. Este nuevo dato será posteriormente utilizado por la unidad de entrada para volver a alimentar la unidad de proceso, y así sucesivamente.
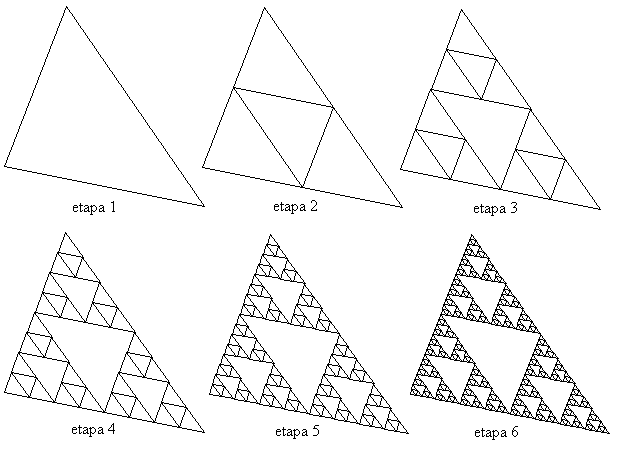
Observamos además que después de un número suficiente de iteraciones el resultado obtenido es prácticamente el mismo, que por cierto responde a un animal matemático con nombre propio, el triángulo de Sierpinski.
También es tan sorprendente como fácilmente comprobable que, tomando una imagen inicial distinta, el resultado “final” es el mismo.
Un grupo de matemáticos comenzó a darse cuenta que en la naturaleza se daba muy seguido el fenómeno de irregularidades y que no eran excepciones como se suponía. Los primeros que comenzaron a demostrar teóricamente esta problemática fueron Cantor (con su famoso y casi místico conjunto de Cantor – Figura 2) y Peano. Hasta llegar a los años de 1880 con Poincaré, al que se lo conoce como el padre de la Teoría del Caos.
Conjunto de Cantor
El mismo también lo estudiaremos con detalle desde el punto de vista puramente matemático y crearemos los algoritmos para generarlo en clases posteriores. Discutiremos si realmente puede ser considerado un fractal de acuerdo a la dimensión fractal que posee.
|
Segun lo antes mencionado . . .
¿Que es Geometria Fractal?
No hay comentarios.:
Publicar un comentario